Nom et prénom :
Comme toujours, la clarté des raisonnements et la précision des notations employées fait partie des critères évalués.
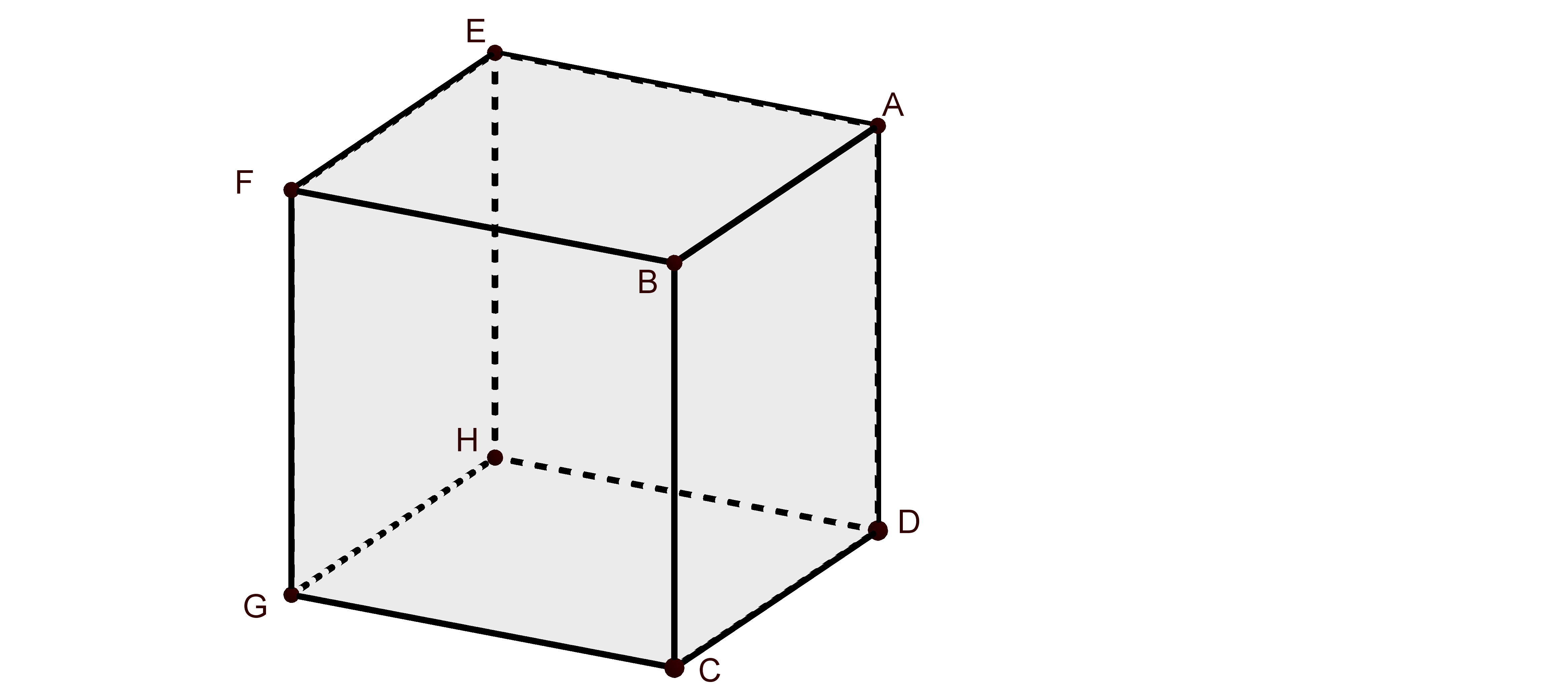
$ABCDEFGH$ est un cube.

$I$ et $J$ sont deux points définis respectivement par $\overrightarrow{EI}=\frac{1}{3}\overrightarrow{EF}$ et $\overrightarrow{GJ}=\frac{2}{3}\overrightarrow{GC}$
Questions :
Première méthode vectorielle (sans coordonnées) $\overrightarrow{IF}$ $=\overrightarrow{IE}+\overrightarrow{EC}+\overrightarrow{CJ}$ (Chasles) $=\overrightarrow{IE}+\overrightarrow{CJ} + \overrightarrow{EC}$ (commutativité de +) $=\frac{1}{3}\overrightarrow{FE}+\frac{1}{3}\overrightarrow{CG}+\overrightarrow{EC}$ (énoncé) $=\frac{1}{3}\overrightarrow{CD}+\frac{1}{3}\overrightarrow{DH}+\overrightarrow{EC}$ (propriétés du cube) $=\frac{1}{3}(\overrightarrow{CD}+\overrightarrow{DH})+\overrightarrow{EC}$ $=\frac{1}{3}\overrightarrow{CH}+\overrightarrow{EC}$ (Chasles) $=\frac{1}{3}\overrightarrow{CE}+\frac{1}{3}\overrightarrow{EH}+\overrightarrow{EC}$ (Chasles) $=\frac{1}{3}\overrightarrow{CE}+\frac{1}{3}\overrightarrow{FG}+\overrightarrow{EC}$ (cube) $=\frac{1}{3}\overrightarrow{CE}+\overrightarrow{EC}+\frac{1}{3}\overrightarrow{FG}$ (commutativité) $=\frac{2}{3}\overrightarrow{EC}+\frac{1}{3}\overrightarrow{FG}$ On a montré que $\overrightarrow{IF}$ est combinaison linéaire de $\overrightarrow{EC}$ et $\overrightarrow{FG}$, donc ces trois vecteurs sont coplanaires.
Seconde méthode (avec des coordonnées) On se place dans un repère, par exemple $(G;\overrightarrow{GC};\overrightarrow{GH};\overrightarrow{GF})$ Les coordonnées de $\overrightarrow{FG}$ sont $(0;0;-1)$, celles de $\overrightarrow{EC}$ sont $(1;-1;-1)$, et celles de $\overrightarrow{IJ}$ sont $(\frac{2}{3};-\frac{2}{3};-1)$ (il faudrait en toute rigueur détailler un peu ces coordonnées à partir de l'énoncé). On cherche deux réels $x$ et $y$ tels que $\overrightarrow{IJ} = x \overrightarrow{FG} + y \overrightarrow{EC}$ ce qui équivaut à $\begin{cases} \frac{2}{3}=x\times 0+y\times \left( 1\right) \\ -\frac{2}{3}=x\times 0+y\times \left( -1\right) \\ -1=x\times \left( -1\right) +y\times \left( -1\right) \end{cases}$ et à $\begin{cases} \frac{2}{3} = y \\ x = 1 - y \end{cases}$ et à $\begin{cases} y = \frac{2}{3}\\ x = \frac{1}{3} \end{cases}$
On a montré que $\overrightarrow{IF}$ est combinaison linéaire de $\overrightarrow{EC}$ et $\overrightarrow{FG}$, donc ces trois vecteurs sont coplanaires.On définit une fonction $g: x \mapsto -2x^3-3x^2+8$. $g$ est une fonction polynôme, donc dérivable sur $\mathbb{R}$. Pour tout $x\in\mathbb{R}$, $g'(x)=-6x^2-6x=-6x(x+1)$. $g$ admet deux racines évidentes : $0$ et $-1$ $g(x)$ est du signe de $-6$ sauf entre ces racines.
On en déduit que $g$ est strictement décroissante sur $]-\infty;-1]$ et sur $[0;+\infty[$, et strictement croissante sur $[-1;0]$.
$g$ admet ainsi un minimum sur $]-\infty;0]$, qui est $g(-1)=7$. $g$ ne s'annule donc pas sur cet intervalle.
Sur $[0;+\infty[$ : 1. $g(0)=8$ et $g(2)=-20$, donc $0 \in [g(2);g(0)]$ 2. $g$ est continue. 3. $g$ est monotone Le corollaire du théorème des valeurs intermédiaires assure l'existence et l'unicité d'une solution $\alpha$ à l'équation $g(x)=0$ sur $[0;2]$.
$g$ étant strictement décroissante sur$[2;+\infty[$, $x>2$ implique que $g(x) < -20$, donc $g$ ne s'annule pas sur cet intervalle.
L'équation n'ayant pas de solution sur $]-\infty;0]$, et une seule sur $[0;+\infty[$, elle en a une unique sur $\mathbb{R}$.
Remarque : on aurait aussi pu appliquer le TVI sur $[0;+\infty[$ en étudiant la limite de $g$ en $+\infty$ (qui est $-\infty$). Il y a unicité car continuité, monotonie et $0 \in ]-\infty;8]$.
On considère la fonction $f: x \mapsto \dfrac{x+1}{x^3+8}$.
$f=\frac{u}{v}$ avec $u:x \mapsto x+1$ et $v: x \mapsto x^3+8$.
$f$ est dérivable sur $]-\infty;-2[$ et sur $]-2;+\infty[$ en tant que quotient de deux fonctions polynômes qui le sont sur ces intervalles où le dénominateur ne s'annule pas.
Pour tout $x$ dans ces intervalles, on a : $f'(x)=\dfrac{1\times(x^3+8)-3x^2(x+1)}{(x^3+8)^2}=\dfrac{-2x^3-3x^2+8}{(x^3+8)^2}=\dfrac{g(x)}{(x^3+8)^2}$.
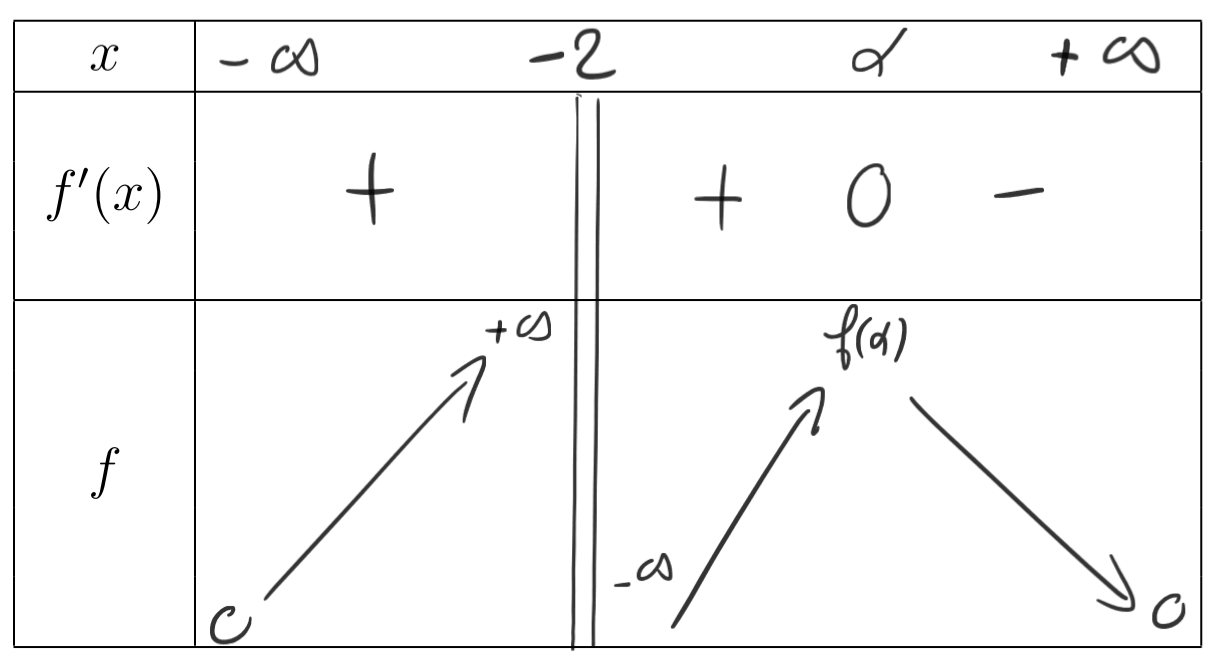
La méthode la plus simple est algébrique : $f(x)=0$ équivaut à $x+1=0$, en multipliant l'équation par $x^3+8$ qui est bien non nul sur $D_f$. La seule solution est donc $-1$, qui n'est pas dans l'intervalle de recherche.
On peut aussi utiliser la notion de limite, associée à la stricte décroissance de la fonction . : Supposons qu'il existe une valeur $z\in[0;+\infty[$ telle que $f(z)=0$. $f$ étant strictement décroissante sur $[0;+\infty[$, $f(z+1) < 0$. On note $M = f(z+1)$. Pour tout $x > z$, on a $f(x) < M$, donc il n'existe aucune valeur de $f(x)$ dans l'intervalle $ ]-M;M[ $. Cela contredit le fait que $ \displaystyle \lim_{x \to +\infty} {f(x)}=0$.