-
-
Dérivation $f$ est un quotient de fonctions dérivables dont le dénominateur ne s'annule pas sur $D_f$ : elle est donc dérivable sur $[0;+\infty[$. On a $f=6-5\times \frac{1}{v}$ où $v: x \mapsto x+1$ et $v': x \mapsto 1$. On a donc, pour tout $x\in D_f$, $f'(x)=-5 \times \frac{-1}{(x+1)^2}=\frac{5}{(x+1)^2}$.
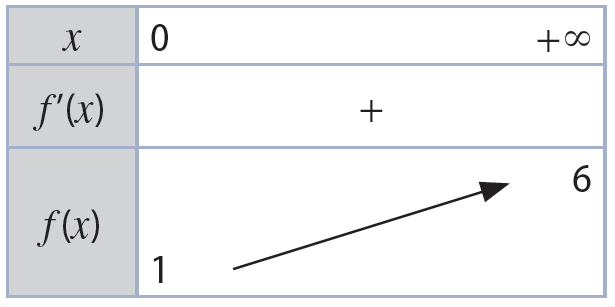
Sens de variation Le dénominateur étant un carré qui ne s'annule pas sur $D_f$, $f'(x)$ est positive, et par conséquent $f$ est croissante sur son ensemble de définition.
Limite en $+\infty$ On sait que $\displaystyle \lim_{x \to +\infty} {x+1} = +\infty$. D'après le théorème de quotient des limites, on a $\displaystyle \lim_{x \to +\infty} \frac{5}{x+1} = 0$, et avec le théorème de somme des limites : $\displaystyle \lim_{x \to +\infty} {f(x)}=6$.
On peut résumer ces résultats dans un tableau de variations :
-
On résout $f(x)=x$ pour $x \in D_f$,
qui équivaut à$f(x)-x=0$et à$6-x -\frac{5}{x+1}=0$et à$(6-x)(x+1)-5=0$en mulitpliant par $(x+1)$ qui est non nul sur $D_f$.et à$-x^2+5x+1=0$
Le discriminant est égal à 29. Le polynôme a deux racines : $x_1=\frac{-5-\sqrt{29}}{2}$ et $x_2=\frac{-5+\sqrt{29}}{2}$.
Seul $x_2$ appartient à $D_f$, donc $f(x)=x$ a une unique solution dans $D_f$ qui est $\frac{-5+\sqrt{29}}{2}$, que l'on note $\alpha$ pour la suite.
-
Pour $x \in [0;\alpha]$, on a $0 \leqslant x \leqslant \alpha$. $f$ étant croissante sur $D_f$, l'ordre est conservé pour les images : $f(0) \leqslant f(x) \leqslant f(\alpha)$, donc $1 \leqslant f(x) \leqslant f(\alpha)=\alpha$, ce qui garantit que $0 \leqslant f(x) \leqslant \alpha$.
De la même façon, si $x \geqslant \alpha$, on a $f(x) \geqslant f(\alpha)=\alpha$, donc $x \in [\alpha;+\infty]$.
-
-
-
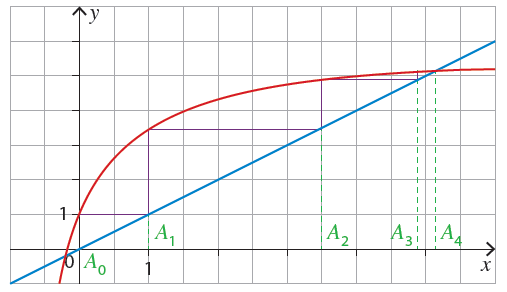 On peut penser que la suite converge vers $\alpha$ en croissant.
On peut penser que la suite converge vers $\alpha$ en croissant.
-
On montre par récurrence la proposition $P_n$: "$0 \leqslant u_n \leqslant u_{n+1} \leqslant \alpha$", pour $n\in\mathbb{N}$.
Initialisation (pour $n=0$). On a $u_0=0$, et on calcule $u_1=f(u_0)=1$. Cela permet de vérifier que $0 \leqslant u_0 \leqslant u_{1} \leqslant \alpha$.
Hérédité On suppose pour un $n$ fixé le temps du raisonnement sur l'hérédite que $0 \leqslant u_n \leqslant u_{n+1} \leqslant \alpha$. On doit vérifier que $0 \leqslant u_{n+1} \leqslant u_{n+2} \leqslant \alpha$ En partant de $P_n$, sachant que $f$ est croissante sur son ensemble de définition, on obtient : $f(0) \leqslant f(u_n) \leqslant f(u_{n+1}) \leqslant f(\alpha)$ et donc que $0 < 1 \leqslant u_{n+1} \leqslant u_{n+2} \leqslant \alpha$. Cela assure que $P_{n+1}$ est vérifiée.
Conclusion : on a montré par récurrence que $P_n$ est vraie pour tout $n\in\mathbb{N}$.
-
Le 2.b justifie que $u$ est croissante et majorée par $\alpha$. La suite est donc convergente (Attention : on ne peut pas savoir à ce stade si sa limite est $\alpha$).
On sait à présent que la limite de $u$ existe. On la nomme $L$. On a ainsi $\displaystyle \lim_{n \to +\infty} {u_n}=L$. La fonction $f$ étant continue sur $D_f$, la suite $(f(u_n))$ est aussi convergente, et par composition, converge vers $f(L)$. Or si $(u_n)$ converge vers $L$, $(u_{n+1})$ aussi : $\displaystyle \lim_{n \to +\infty} {u_n} = \displaystyle \lim_{n \to +\infty} {u_{n+1}}$. La limite $L$ est donc telle que $f(L)=L$, et d'après la question 1, il n'y a qu'une solution à cette équation : $L=\alpha$.
On a montré que $(u_n)$ converge, et que sa limite est bien $\alpha$.
Remarque : le raisonnement ci-dessus est très classique, et très efficace.
-
-
En reprenant l'étude du 1.b sur le trinôme $-x^2+5x+1$, on établit que $f(x)-x$ est négatif sauf entre ses racines.
Restreint à $[0;+\infty]$, on peut en déduire que :
- Si $x \in [0;\alpha[$, $f(x)-x > 0$ donc $f(x) > x$.
- Si $x = \alpha$, $f(x)-x = 0$ donc $f$ est constante, égale à $\alpha$.
- Si $x \in ]\alpha;+\infty[$, $f(x)-x < 0$ donc $f(x) < x$.
- Si $x \in [0;\alpha[$, on a $u_1=f(u_0) > u_0$, et en refaisant le raisonnement par récurrence du 2.b, on obtient que la suite est croissante, majorée, puis comme au 2c, qu'elle tend vers $\alpha$.
- Si $x=\alpha$, $f$ est constante et converge donc aussi vers $\alpha$ !
- Si $x \in ]\alpha;+\infty[$, on a $u_1=f(u_0) < u_0$, et en refaisant un raisonnement par récurrence qui ressemble à celui du 2b, on peut montrer que pour tout $n\in\mathbb{N}$, $\alpha \leqslant u_{n+1} \leqslant u_n$. La suite est alors décroissante et minorée, donc convergente, et sa limite est aussi $\alpha$ par le même raisonnement qu'au 2c.